Яблонский задание Д.14. Применение принципа возможных перемещений к решению задач о равновесии сил, приложенных к механической системе с одной

Поиск задач

Найти задачу можно, введя ее условие. Если с первого раза не нашли решение на нужное готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия

Решение задач → Задачи по теоретической механике с решениями

Яблонский задание Д.14. Применение принципа возможных перемещений к решению задач о равновесии сил, приложенных к механической системе с одной степенью свободы.
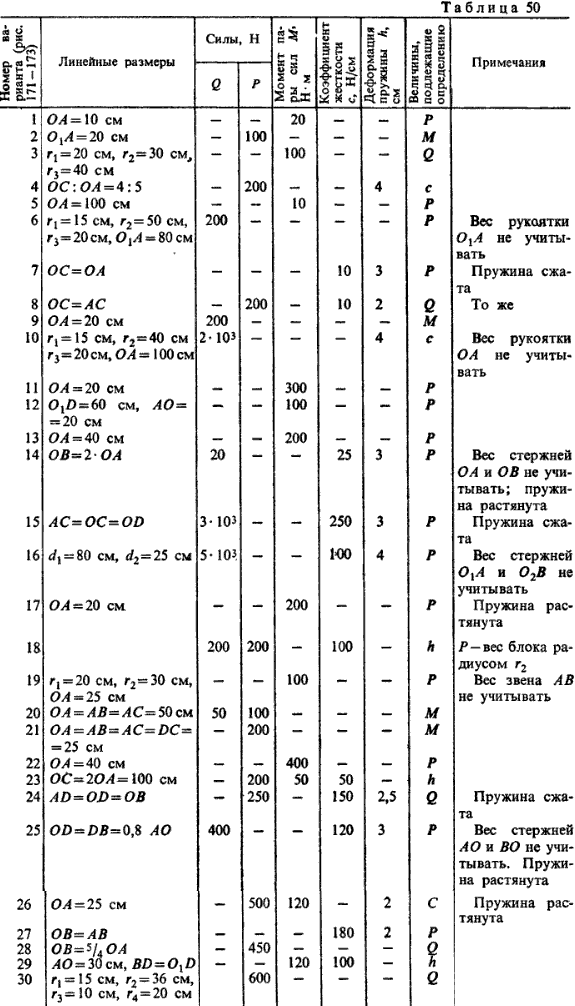
Схемы механизмов, находящихся под действием взаимно уравновешивающихся сил, показаны на рис. 171-173, а необходимые данные приведены в табл. 50.
Применяя принцип возможных перемещений и пренебрегая силами сопротивления, определить величину, указанную в предпоследней графе таблице 50.
Примечание. Механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30 расположены в вертикальной плоскости, а остальные-в горизонтальной.

Пример решения; Вариант 1; Вариант 2; Вариант 3; Вариант 4; Вариант 5; Вариант 6; Вариант 7; Вариант 8; Вариант 9; Вариант 10; Вариант 11; Вариант 12; Вариант 13; Вариант 14; Вариант 15; Вариант 16; Вариант 17; Вариант 18; Вариант 19; Вариант 20; Вариант 21; Вариант 22; Вариант 23; Вариант 24; Вариант 25; Вариант 26; Вариант 27; Вариант 28; Вариант 29; Вариант 30.

Для просмотра изображения в полном размере нажмите на него

Решение задачи 14
(Яблонский)

<< Предыдущее

Следующее >>

Задание Д.13 вариант 29. Маятник, отклоненный от положения устойчивого равновесия на некоторый угол α, падает без начальной скорости под действием собственного веса, вращаясь вокруг неподвижной оси O, и в вертикальном положении точкой A ударяется о покоящийся однородный полый тонкостенный цилиндр массой m0=200 кг и радиусом r=0,2 м. Масса маятника m=100 кг, радиус его инерции относительно оси вращения i0=1 м. Расстояния от точки O пересечения оси вращения вертикальной плоскостью симметрии до центра тяжести C маятника и до точки A, находящейся в той же плоскости симметрии, OC=d=0,8 м и OA=l=1,2 м. Коэффициент восстановления при соударении маятника и цилиндра k=0,6. После удара цилиндр скользит, не вращаясь, по гладкой горизонтальной плоскости и, натолкнувшись на ступеньку DE высотой h=0,05 м, поднимается на нее, не перемещаясь дальше ребра E. Отрыва цилиндра от ребра E при ударе о ступеньку не происходит, а абсолютно шероховатая поверхность ступеньки исключает проскальзывание цилиндра при ударном воздействии. Определить угол α первоначального отклонения маятника, а также ударный импульс, испытываемый цилиндром со стороны маятника.

Задание Д.13 вариант 30. Рычаг состоит из двух абсолютно жестких стержней OD и OF, соединенных под прямым углом; OD=a=1 м, OF=b=1,5 м. Рычаг имеет шарнирно-неподвижную опору O и удерживается в точке E пружиной. Масса рычага m=400 кг, радиус его инерции относительно оси вращения O i0=0,4 м. Рычаг находится в покос, соответствующем статической деформации пружины, при этом его стержень OD горизонтален. В точку D рычага падает груз A массой mA=20 кг с высоты h=0,5 м. Удар груза о стержень OD рычага-неупругий (k1=0). Приобретя угловую скорость, рычаг точкой F ударяется о неподвижное тело B массой mB=120 кг; коэффициент восстановления при этом ударе k2=0,2. Считать груз A и тело B материальными точками. Определить, какую скорость получает тело B в конце его соударения со стержнем OF, а также ударный импульс, воспринимаемый телом B.

Д14 пример 1. Дано: Q=100 Н; c=5 Н/см; r1=20 см; r2=40 см; r3=10 см; OA=l=50 см; α=30°; β=90° (рис. 174). Определить деформацию h пружины, пренебрегая весом звеньев OA и AB.

Задание Д.14 вариант 1. OA=10 см M=20 Н*м, подлежит определению: P;

online-tusa.com | SHOP