Решение задач → Задачи по геометрии с решениями
В трапеции ABCD с основаниями AD и BC диагонали AC и BD пересекаются в точке E. Вокруг треугольника ECB описана окружность, а касательная к этой окружности, проведённая в точке E, пересекает прямую AD в точке F таким образом, что точки A, D и F лежат последовательно на этой прямой. Известно, что AF=a, AD=b. Найдите EF.
Для просмотра изображения в полном размере нажмите на него 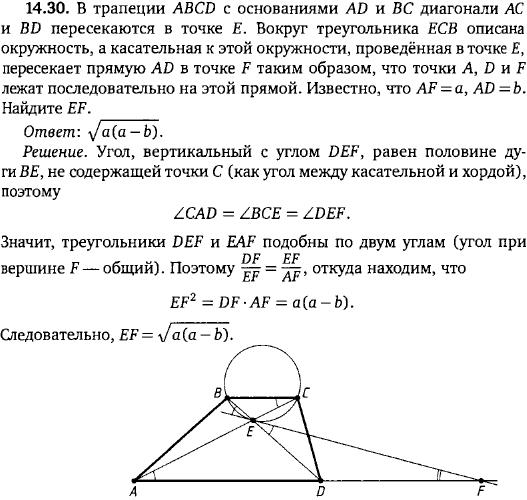 |
Решение задачи 14.30
(ЕГЭ 2012. Математика. Решение задачи С4)
| << Предыдущее
|
Следующее >>
|
|
14.28. Радиус окружности, описанной около треугольника KLM, равен R. Через вершину L проведена прямая, перпендикулярная стороне KM. Эту прямую пересекают в точках A и B серединные перпендикуляры к сторонам KL и LM соответственно. Известно, что AL=a. Найдите BL.
|
14.29. В окружности проведены диаметр MN и хорда AB, параллельная диаметру MN. Касательная к окружности в точке M пересекает прямые NA и NB соответственно в точках P и Q. Известно, что MP=p, MQ=q. Найдите MN.
|
14.31. В трапеции ABCD известно, что BC параллельна AD, угол ∠ABC=90°. Прямая, перпендикулярная стороне CD, пересекает сторону AB в точке M, а сторону CD-в точке N. Известно также, что MC=a, BN=b, а расстояние от точки D до прямой MC равно c. Найдите расстояние от точки A до прямой BN.
|
14.32. В треугольник ABC со сторонами AB=6, BC=5, AC=7 вписан квадрат, две вершины которого лежат на стороне AC, одна на стороне AB и одна на стороне BC. Через середину D стороны AC и центр квадрата проведена прямая, которая пересекается с высотой BH треугольника ABC в точке M. Найдите площадь треугольника DMC.
|
|