Механическая система с одной степенью свободы (рис. 251-253) может совершать колебания относительно положения равновесия. В начальный момент (t=0) система выведена из положения равновесия и скорости всех ее точек равны нулю. Предоставленная далее самой себе система колеблется, находясь под действием только консервативных сил.
В схемах вариантов 8 и 20 применены пружины, сила упругости которых связана с деформацией λ соотношением P(λ)=cλ + αλ3. В остальных схемах использованы пружины, для которых зависимость силы упругости P от деформации λ-линейная, т. е. P=cλ. В вариантах 3, 4, 7, 9-11, 21, 22 пружины имеют деформацию f в положении покоя (предварительный натяг). В схемах вариантов 12-17, 23-28 пружины установлены с зазором s. λ В задании требуется:
1. Составить Дифференциальное уравнение, описывающее движение системы (свободные колебания системы).
2. Численным интегрированием на ЭВМ найти решение дифференциального уравнения при заданных начальных условиях.
3. По результатам численного интегрирования определить циклическую частоту k и период T колебаний.
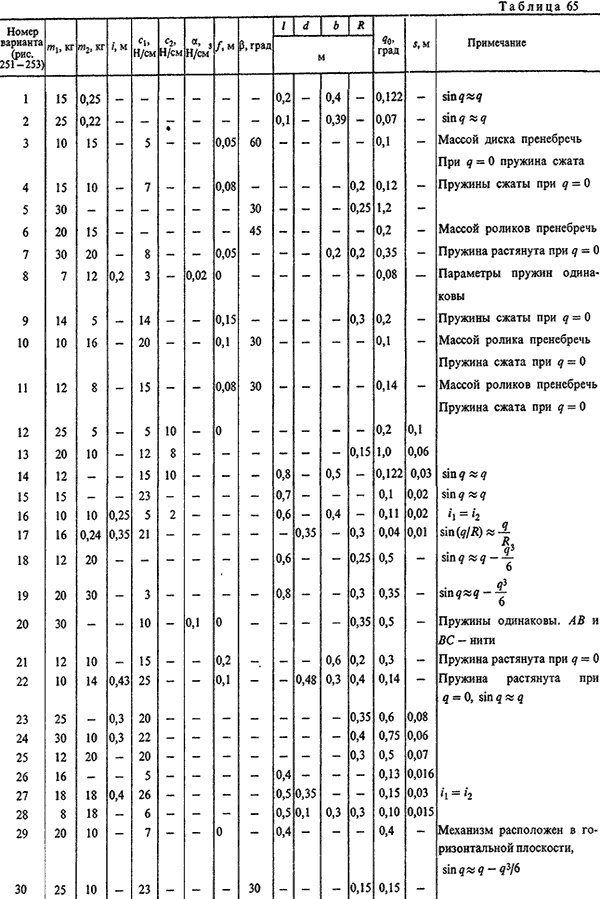
Схемы механических систем приведены на рис. 251-253 в положении покоя. На каждой схеме указана координата, которую нужно принять в качестве обобщенной. Необходимые для расчета данные приведены в таблице 65. Здесь m1, m2-массы тел системы; i-радиус инерции тела, участвующего во вращательном движении относительно центральной оси; c1, c2-коэффициенты жесткости для линейных пружин; c1 и α-коэффициенты для определения зависимости силы упругости от деформации для нелинейных пружин, f-деформация пружины в положении покоя (в примечании указано, сжата пружина или растянута); q0-начальное значение обобщенной координаты, s-величина зазора, d-расстояние от оси вращения до центра тяжести тела. Качение тел во всех случаях происходит без проскальзывания. Тела, для которых радиус инерции не указан, считать сплошными цилиндрами.
Примечание. В вариантах 7, 21 и 22 выражение для обобщенной силы разложить в ряд Маклорена и удержать члены не выше третьего порядка малости относительно обобщенной координаты. В вариантах 1 и 2 принять, что колебания «перевалки» вокруг опорных ребер происходят без потери энергии.
Пример решения; Вариант 1; Вариант 2; Вариант 3; Вариант 4; Вариант 5; Вариант 6; Вариант 7; Вариант 8; Вариант 9; Вариант 10; Вариант 11; Вариант 12; Вариант 13; Вариант 14; Вариант 15; Вариант 16; Вариант 17; Вариант 18; Вариант 19; Вариант 20; Вариант 21; Вариант 22; Вариант 23; Вариант 24; Вариант 25; Вариант 26; Вариант 27; Вариант 28; Вариант 29; Вариант 30;