В данную окружность впишите прямоугольный треугольник, катеты которого проходят через две данные точки внутри окружности.

Поиск задач

Найти задачу можно, введя ее условие. Если с первого раза не нашли решение на нужное готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия

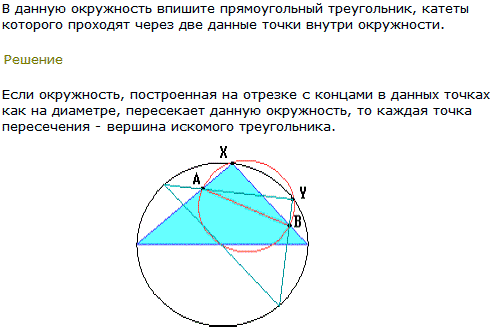
Решение задач → Задачи по геометрии с решениями

Для просмотра изображения в полном размере нажмите на него

В данную окружность впишите прямоугольный треугольник, катеты которого проходят через две данные точки внутри окружности.

Решение задачи 2.3
(Пособие для абитуриентов и старших классов)

<< Предыдущее

Следующее >>

2.1. Пусть M и N-середины сторон CD и DE правильного шестиугольника ABCDEF, P-точка пересечения отрезков AM и BN. Докажите, что S(ABP)=S(MDNP)

2.2. В окружность радиуса 2√7 вписана трапеция ABCD, причем ее основание AD является диаметром, а угол BAD равен 60o. Хорда CE пересекает диаметр AD в точке P такой, что AP:PD=1:3. Найдите площадь треугольника BPE.

2.4 На дуге BC окружности, описанной около равностороннего треугольника ABC, взята произвольная точка P. Докажите, что AP=BP + CP.

2.5 AA1 и BB1-высоты остроугольного треугольника ABC. Докажите, что: а) треугольник AA1C подобен треугольнику BB1C; б) треугольник ABC подобен треугольнику A1B1C.

online-tusa.com | SHOP