Решение задач → Задачи по теоретической механике с решениями
Груз P массы m подвешен к стержню AB, который соединен двумя пружинами, с коэффициентами жесткости c2 и c3, со стержнем DE. Последний прикреплен к потолку в точке Н пружиной, коэффициент жесткости которой c1. При колебаниях стержни AB и DE остаются горизонтальными. Определить коэффициент жесткости одной эквивалентной пружины, при которой груз P будет колебаться с той же частотой. Найти период свободных колебаний груза. Массой стержней пренебречь.
Для просмотра изображения в полном размере нажмите на него 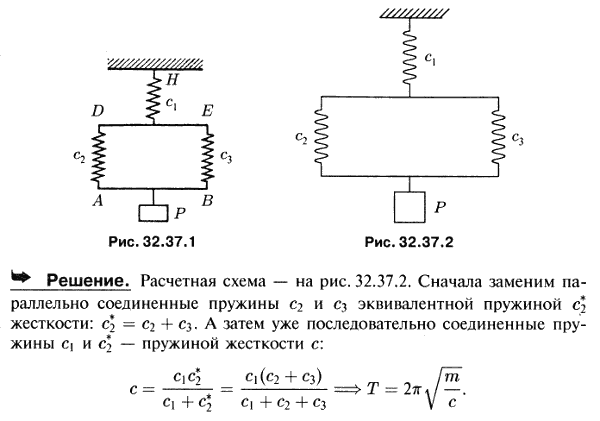 |
Решение задачи 32.37
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
32.35 Винтовая пружина состоит из n участков, коэффициенты жесткости которых соответственно равны c1, c2,..., cn. Определить коэффициент жесткости c однородной пружины, эквивалентной данной, и период свободных колебаний точки, масса которой равна m.
|
32.36 Груз массы 10 кг, лежащий на абсолютно гладкой горизонтальной плоскости зажат между двумя пружинами одинаковой жесткости c=19,6 Н/см. В некоторый момент груз был сдвинут на 4 см от положения равновесия вправо и отпущен без начальной скорости. Найти уравнение движения, период колебаний, а также максимальную скорость груза.
|
32.38 Определить собственную частоту колебаний груза Q массы m, подвешенного на конце упругой консоли длины l. Пружина, удерживающая груз, имеет жесткость c. Жесткость на конце консоли определяется формулой c1=3EJ/l3 (E-модуль упругости, J-момент инерции). Массой консоли пренебречь.
|
32.39 Колебания груза массы M=10 кг, лежащего на середине упругой балки жесткости c=20 Н/см, происходят с амплитудой 2 см. Определить величину начальной скорости груза, если в момент времени t=0 груз находился в положении равновесия.
|
|