Решение задач → Задачи по геометрии с решениями
Отношение радиусов окружностей S1 и S2, касающихся в точке B, равно k (k > 1). Из точки A, лежащей на окружности S1, проведена прямая, касающаяся окружности S2 в точке C. Найдите AC, если известно, что хорда, высекаемая окружностью S2 на прямой AB, равна b.
Для просмотра изображения в полном размере нажмите на него 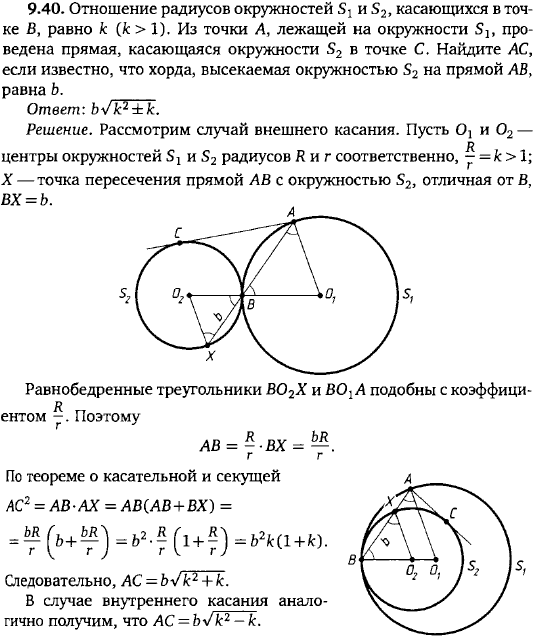 |
Решение задачи 9.40
(ЕГЭ 2012. Математика. Решение задачи С4)
| << Предыдущее
|
Следующее >>
|
|
9.38. Окружности радиусов r и R касаются друг друга внутренним образом. Найдите сторону правильного треугольника, у которого одна вершина находится в точке касания данных окружностей, а две другие лежат на разных данных окружностях.
|
9.39. Радиусы окружностей S1 и S2, касающихся в точке A, равны R и r (R > r). Прямая, проходящая через точку B, лежащую на окружности S1, касается окружности S2 в точке C. Найдите BC, если известно, что AB=a.
|
9.41. Окружность радиуса 1 касается окружности радиуса 3 в точке C. Прямая, проходящая через точку C, пересекает окружность меньшего радиуса в точке A, а большего радиуса-в точке B. Найдите AC, если AB=2√5.
|
9.42. Окружность радиуса 2 касается окружности радиуса 4 в точке B. Прямая, проходящая через точку B, пересекает окружность меньшего радиуса в точке A, а окружность большего радиуса-в точке C. Найдите BC, если AC=3√2.
|
|