Решение задач → Задачи по теоретической механике с решениями
Задание Д.3 вариант 29. Плита лежит на двух одинаковых параллельных пружинах 1 и 2, коэффициенты жесткости которых c1=c2=c=400 Н/см. В некоторый момент времени груз D (m=200 кг) устанавливают на середину плиты и одновременно прикрепляют к недеформированной пружине 3, имеющей коэффициент жесткости c3=200 Н/см. В тот же момент времени (при недеформированных пружинах) грузу сообщают скорость v0=0,6 м/с, направленную вниз.
Для просмотра изображения в полном размере нажмите на него 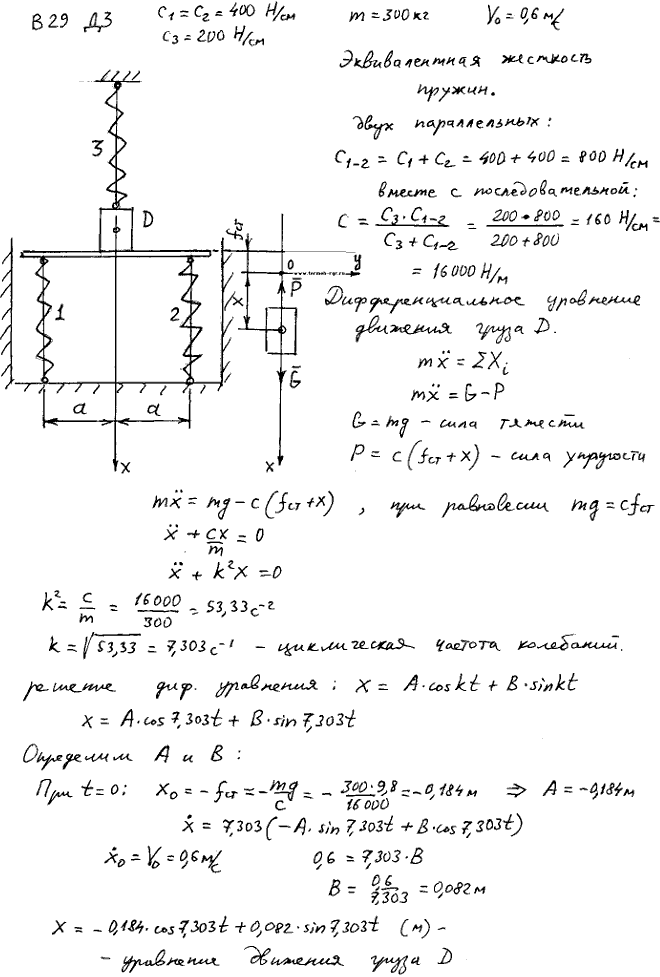 |
Решение задачи 3.29
(Яблонский)
| << Предыдущее
|
Следующее >>
|
|
Задание Д.3 вариант 27. Коэффициент жесткости каждой из двух параллельных пружин, на которых лежит плита, c=130 Н/см. Груз D (m=40 кг) устанавливают на середину плиты и отпускают без начальной скорости при недеформированных пружинах. Сопротивление движению груза пропорционально скорости: R=400v, где v-скорость. Массой плиты и демпфера пренебречь.
|
Задание Д.3 вариант 28. Груз D падает на плиту с высоты h=5 см. Статический прогиб пружины под действием этого груза fст=1 см.
|
Задание Д.3 вариант 30. В некоторый момент времени груз D (m=100 кг) устанавливают на плиту и отпускают (при недеформированной пружине) без начальной скорости. В этот же момент времени точка B (нижний конец пружины) начинает совершать движение по вертикали согласно закону ξ=0,5sin 20t (см) (ось ξ направлена вниз). Коэффициент жесткости пружины c=2000 Н/см. Примечание. Начало отсчета на оси x соответствует среднему положению точки B (ξ=0).
|
Яблонский задание Д.4. Исследование относительного движения материальной точки. Шарик M, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела A (рис. 129-131). Найти уравнение относительного движения этого шарика x=f(t), приняв за начало отсчета точку O. Тело A равномерно вращается вокруг неподвижной оси (в вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения z1 вертикальна, в вариантах 1, 12, 15 и 25 ось вращения x1 горизонтальна). В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29 тело A движется поступательно, параллельно вертикальной плоскости y1O1z1. Найти также координату x и давление шарика на стенку канала при заданном значении t=t1. Данные, необходимые для выполнения задания, приведены в табл. 40. В задании приняты следующие обозначения: m-масса шарика M; ω-постоянная угловая скорость тела A (в вариантах 1-4, 7, 10-12, 14, 15, 20, 23, 25, 26, 30) или кривошипов O1B и O2C (в вариантах 6, 17, 22); c-коэффициент жесткости пружины, к которой прикреплен шарик M; l0-длина недеформированной пружины; f-коэффициент трения скольжения шарика по стенке канала; x0, x'0-начальная координата и проекция начальной скорости на ось x. Пример решения; Вариант 1; Вариант 2; Вариант 3; Вариант 4; Вариант 5; Вариант 6; Вариант 7; Вариант 8; Вариант 9; Вариант 10; Вариант 11; Вариант 12; Вариант 13; Вариант 14; Вариант 15; Вариант 16; Вариант 17; Вариант 18; Вариант 19; Вариант 20; Вариант 21; Вариант 22; Вариант 23; Вариант 24; Вариант 25; Вариант 26; Вариант 27; Вариант 28; Вариант 29; Вариант 30;
|
|