Решение задач → Задачи по теоретической механике с решениями
Электродвигатель ЭД стабилизирующего привода установлен на вращающейся раме, положение которой задается углом φ. Шестерня 1 на валу электродвигателя обкатывается вокруг шестерни 2, связанной с неподвижным основанием. Составить дифференциальное уравнение движения рамы, если J1-момент инерции рамы вместе с электродвигателем, J0-момент инерции ротора электродвигателя, i12-передаточное число пары шестерен, M0-вращающий момент электродвигателя, M'0-момент сил сопротивления на валу электродвигателя, M'1-момент сил, приложенных к раме вокруг ее оси.
Для просмотра изображения в полном размере нажмите на него 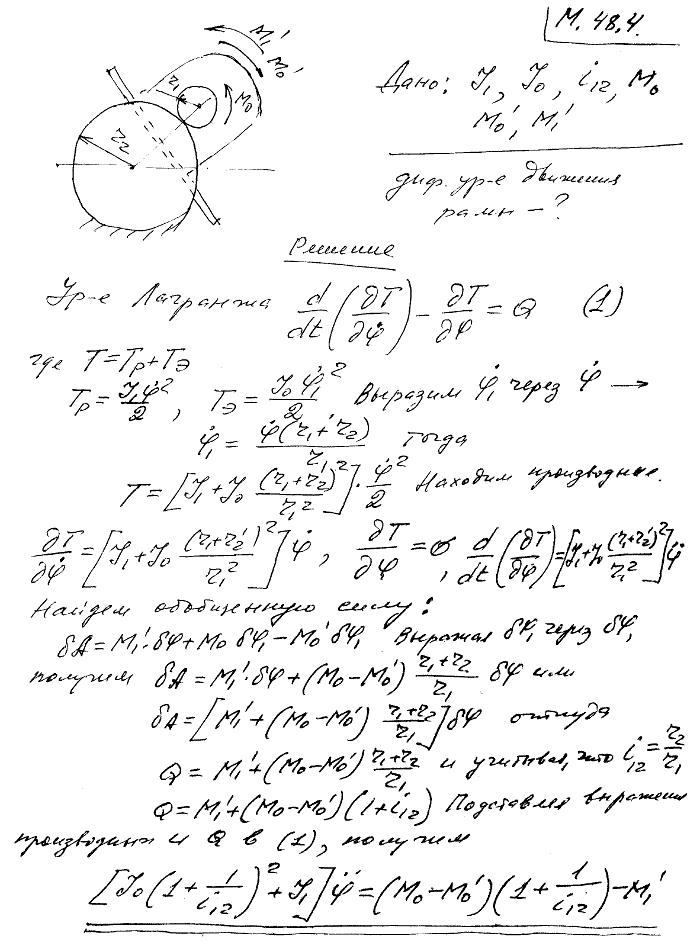 |
Решение задачи 48.4
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
48.2 Барабан Б центрифуги приводится во вращение электродвигателем ЭД через двухступенчатый редуктор. Заданы момент инерции J0 электродвигателя, момент инерции J2 барабана, момент инерции J1 промежуточного вала редуктора, передаточные числа i01 и i12 ступеней редуктора. К ротору электродвигателя приложен вращающий момент M0 и момент сил сопротивления M'0, к валу редуктора и к барабану-моменты сил сопротивления M'1 и M'2 соответственно. Составить дифференциальное уравнение вращения барабана центрифуги.
|
48.3 Привод электромобиля состоит из электродвигателя ЭД и одноступенчатого редуктора с передаточным числом i. Составить дифференциальное уравнение движения электромобиля, если J0-момент инерции ротора электродвигателя, J1-момент инерции каждого из четырех колес, имеющих радиус r, m-суммарная масса электромобиля, M-вращающий момент электродвигателя, M'-момент сил сопротивления на валу электродвигателя, F-суммарная сила сопротивления движению электромобиля.
|
48.5 Определить движение груза массы m, висящего на однородном тросе массы m1 и длины l; трос навернут на барабан радиуса a и массы m2; ось вращения горизонтальна; трением пренебречь, массу барабана считать равномерно распределенной по его ободу. В начальный момент t=0 система находилась в покое, длина свисавшей части троса l0.
|
48.6 В эпициклическом механизме бегающая шестеренка радиуса r1 насажена на кривошип с противовесом, вращающийся вокруг оси неподвижной шестеренки под действием приложенного момента M. Определить угловое ускорение вращения кривошипа и окружное усилие S в точке касания шестеренок, если расстояние между осями шестеренок равно l, момент инерции кривошипа с противовесом относительно оси вращения кривошипа равен J0, масса бегающей шестеренки m1, момент инерции шестеренки относительно ее оси J1; трением пренебречь, центр масс шестеренки и кривошипа с противовесом находится на оси вращения кривошипа.
|
|