Решение задач → Задачи по теоретической механике с решениями
В вибрографе для записи горизонтальных колебаний фундаментов машин маятник OA, состоящий из рычага с грузом на конце, может качаться вокруг своей горизонтальной оси O, удерживаясь в вертикальном положении устойчивого равновесия собственной массой и спиральной пружиной. Определить период собственных колебаний маятника при малых углах отклонения, если максимальный статический момент силы тяжести маятника относительно его оси вращения равен Mgh, момент инерции относительно той же оси равен Jz, коэффициент жесткости пружины, сопротивление которой пропорционально углу закручивания, равен c; при равновесном положении маятника пружина находится в ненапряженном состоянии. Сопротивлениями пренебречь.
Для просмотра изображения в полном размере нажмите на него 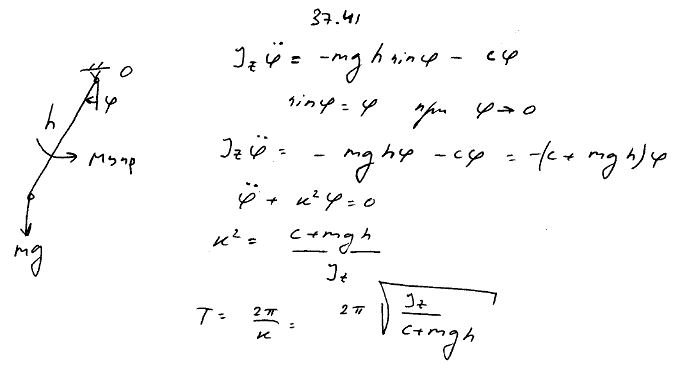 |
Решение задачи 37.41
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
37.39 Найти уравнение малых колебаний однородного диска массы M и радиуса r, совершающего колебания вокруг горизонтальной оси Oz, перпендикулярной его плоскости и отстоящей от центра масс C диска на расстоянии OC=r/2. К диску приложен вращающий момент mвр, причем mвр z=m0 sin pt, где m0 и p-постоянные. В начальный момент диску, находившемуся в нижнем положении, была сообщена угловая скорость ω0. Силами сопротивления пренебречь. Считая колебания малыми, принять sin φ≈φ.
|
37.40 В сейсмографах-приборах для регистрации землетрясений-применяется физический маятник, ось подвеса которого образует угол α с вертикалью. Расстояние от оси подвеса до центра масс маятника равно a, момент инерции маятника относительно оси, проходящей через его центр масс параллельно оси подвеса, равен JC, масса маятника равна M. Определить период колебаний маятника
|
37.42 Виброграф (см. предыдущую задачу) закреплен на фундаменте, совершающем горизонтальные гармонические колебания по закону x=a sin ωt. Определить амплитуду a колебаний фундамента, если амплитуда вынужденных колебаний маятника вибрографа оказалась равной φ0
|
37.43 При пуске в ход электрической лебедки к барабану A приложен вращающий момент mвр, пропорциональный времени, причем mвр=at, где a-постоянная. Груз B массы M1 поднимается посредством каната, навитого на барабан A радиуса r и массы M2. Определить угловую скорость барабана, считая его сплошным цилиндром. В начальный момент лебедка находилась в покое.
|
|