Решение задач → Задачи по теоретической механике с решениями
Часовой балансир A может вращаться вокруг оси, перпендикулярной его плоскости и проходящей через центр тяжести O, имея относительно этой оси момент инерции J. Балансир приводится в движение спиральной пружиной, один конец которой с ним скреплен, а другой присоединен к неподвижному корпусу часов. При повороте балансира возникает момент сил упругости пружины, пропорциональный углу поворота. Момент, необходимый для закручивания пружины на один радиан, равен c. Определить закон движения балансира, если в начальный момент в условиях отсутствия сил упругости балансиру сообщили начальную угловую скорость ω0.
Для просмотра изображения в полном размере нажмите на него 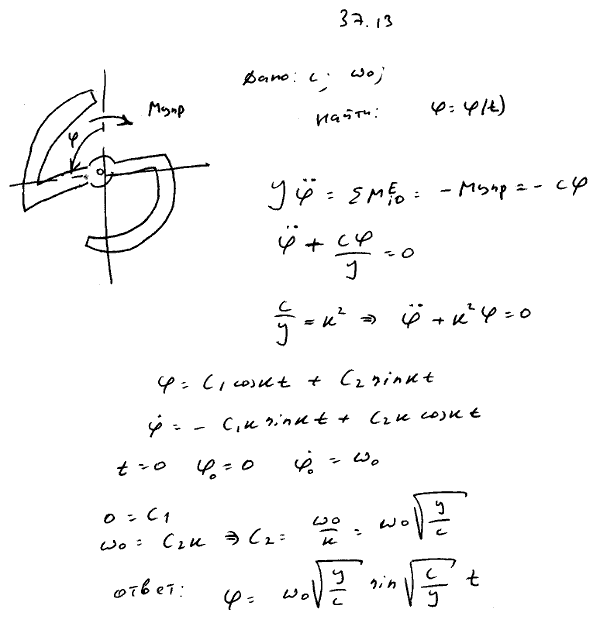 |
Решение задачи 37.13
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
37.11 Вал радиуса r приводится во вращательное движение вокруг горизонтальной оси гирей, подвешенной посредством троса. Для того чтобы угловая скорость вала через некоторое время после начала движения имела величину, близкую к постоянной, с валом соединены n одинаковых пластин; сопротивление воздуха, испытываемое пластиной, приводится к силе, нормальной к пластине, приложенной на расстоянии R от оси вала и пропорциональной квадрату ее угловой скорости, причем коэффициент пропорциональности равен k. Масса гири m, момент инерции всех вращающихся частей относительно оси вращения равен J; массой троса и трением в опорах пренебречь. Определить угловую скорость вала, еслив начальный момент она равна нулю.
|
37.12 Упругую проволоку, на которой подвешен однородный шар с радиусом r и массой m, закручивают на угол φ0, а затем предоставляют ей свободно раскручиваться. Момент, необходимый для закручивания проволоки на один радиан, равен c. Определить движение, пренебрегая сопротивлением воздуха и считая момент силы упругости закрученной проволоки пропорциональным углу кручения φ.
|
37.14 Для определения момента инерции Jz тела A относительно вертикальной оси Oz его прикрепили к упругому вертикальному стержню OO1, закрутили этот стержень, повернув тело A вокруг оси Oz на малый угол φ0, и отпустили; период возникших колебаний оказался равным T1, момент сил упругости относительно оси Oz равен mz=-cφ. Для определения коэффициента c проделали второй опыт: на стержень в точке O был надет однородный круглый диск радиуса r массы M, и тогда период колебаний оказался равным T2. Определить момент инерции тела Jz.
|
37.15 Решить предыдущую задачу в предположении, что для определения коэффициента c второй опыт проделывают иначе: однородный круглый диск массы M и радиуса r прикрепляется к телу, момент инерции которого требуется определить. Найти момент инерции тела Jz, если период колебаний тела τ1, а период колебаний тела с прикрепленным к нему диском τ2.
|
|