Решение задач → Задачи по теоретической механике с решениями
Груз M, подвешенный к неподвижной точке A на пружине, совершает малые гармонические колебания в вертикальной плоскости, скользя без трения по дуге окружности, диаметр которой AB равен l; натуральная длина пружины a; жесткость пружины такова, что при действии силы, равной весу груза M, она получает удлинение, равное b. Определить период T колебаний в том случае, когда l=a+b; массой пружины пренебречь и считать, что при колебаниях она остается растянутой.
Для просмотра изображения в полном размере нажмите на него 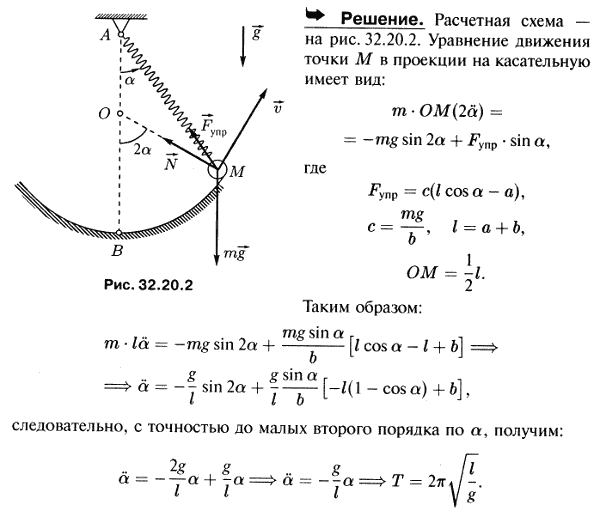 |
Решение задачи 32.20
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
32.18 Тело массы M=12 кг, прикрепленное к концу пружины, совершает гармонические колебания. При помощи секундомера установлено, что тело совершило 100 полных колебаний за 45 c. После этого к концу пружины добавочно прикрепили груз массы M1=6 кг. Определить период колебаний двух грузов на пружине.
|
32.19 В условиях предыдущей задачи найти уравнение движения одного груза M и двух грузов M+M1, если в обоих случаях грузы были подвешены к концу нерастянутой пружины.
|
32.21 В условиях предыдущей задачи найти уравнение движения груза M, если в начальный момент ∠BAM=φ0 и точке M сообщили начальную скорость v0, направленную по касательной к окружности вниз.
|
32.22 Тело E, масса которого равна m, находится на гладкой горизонтальной плоскости. К телу прикреплена пружина жесткости c, второй конец которой прикреплен к шарниру O1. Длина недеформированной пружины равна l0; в положении равновесия имеет конечный предварительный натяг, равный F0=c(l-l0), где l=OO1. Учитывая в горизонтальной составляющей упругой силы пружины лишь линейные члены относительно отклонения тела от положения равновесия, определить период малых колебаний тела.
|
|