Решение задач → Задачи по теоретической механике с решениями
Две частицы заряжены положительным электричеством, заряд первой частицы q1=100 Кл, заряд второй частицы q2=0,1q1, первая частица остается неподвижной, а вторая движется вследствие силы отталкивания от первой частицы. Масса второй частицы равна 1 кг, начальное расстояние от первой частицы равно 5 м, а начальная скорость равна нулю. Определить верхний предел для скорости движущейся частицы, принимая во внимание действие только одной силы отталкивания F=q1q2/r2, где r-расстояние между частицами.
Для просмотра изображения в полном размере нажмите на него 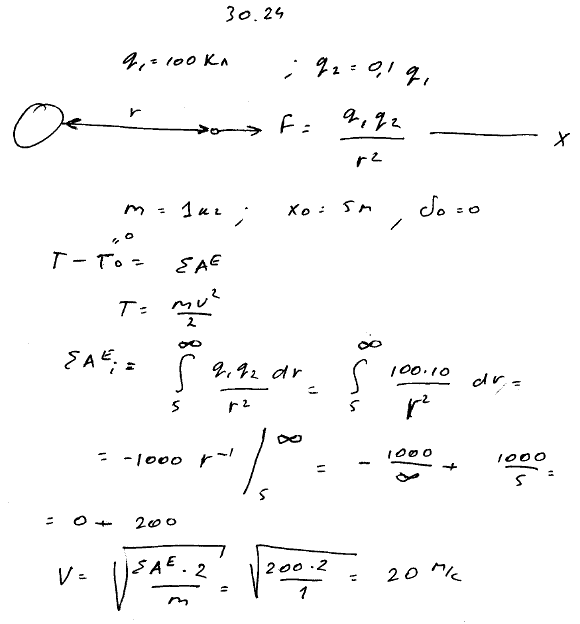 |
Решение задачи 30.24
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
30.22 Горизонтальная пружина, на конце которой прикреплена материальная точка, сжата силой P и находится в покое. Внезапно сила P меняет направление на прямо противоположное. Определить, пренебрегая массой пружины, во сколько раз получающееся при этом наибольшее растяжение l2 больше первоначального сжатия l1.
|
30.23 Тело брошено с поверхности Земли вверх по вертикальной линии с начальной скоростью v0. Определить высоту H поднятия тела, принимая во внимание, что сила тяжести изменяется обратно пропорционально квадрату расстояния от центра Земли; сопротивлением воздуха пренебречь. Радиус Земли R=6370 км, v0=1 км/с.
|
30.25 Определить скорость v0, которую нужно сообщить по вертикали вверх телу, находящемуся на поверхности Земли, для того, чтобы оно поднялось на высоту, равную земному радиусу; при этом нужно принять во внимание только силу притяжения Земли, которая изменяется обратно пропорционально квадрату расстояния тела от центра Земли. Радиус Земли равен 6,37*106 м, ускорение силы притяжения на поверхности Земли равно 9,8 м/с2.
|
30.26 Найти, с какой скоростью v0 нужно выбросить снаряд с поверхности Земли по направлению к Луне, чтобы он достиг точки, где силы притяжения Земли и Луны равны, и остался в этой точке в равновесии. Движением Земли и Луны и сопротивлением воздуха пренебречь. Ускорение силы тяжести у поверхности Земли g=9,8 м/с2. Отношение массы Луны и Земли m:M=1:80; расстояние между ними d=60R, где считаем R=6000 км (радиус Земли). Коэффициент f, входящий в формулу для величины силы всемирного тяготения, находим из уравнения mg=mf[M/R2-m/(d-R)2].
|
|