Решение задач → Задачи по теоретической механике с решениями
Две ненапряженные пружины AC и BC, расположенные по горизонтальной прямой Ax, прикреплены шарнирами к неподвижным точкам A и B, а в точке C-к гире массы 2 кг. Пружина AC сжимается на 1 см силой 20 Н, а пружина CB вытягивается на 1 см силой 40 Н. Расстояние AC=BC=10 см. Гире C сообщена скорость v0=2 м/с в таком направлении, что при последующем движении она проходит через точку D, координаты которой xD=8 см, yD=2 см, если за начало координат принять точку A и координатные оси направить, как указано на рисунке. Определить скорость гири в момент прохождения ее через точку D, лежащую в вертикальной плоскости xy.
Для просмотра изображения в полном размере нажмите на него 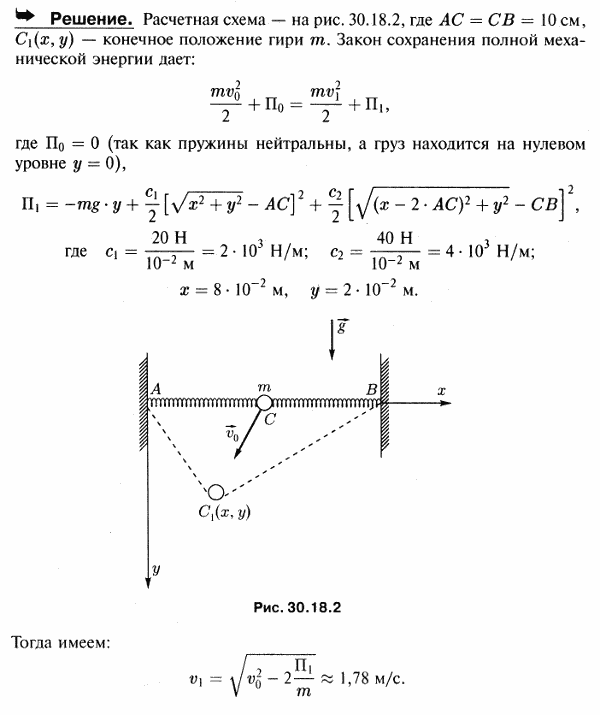 |
Решение задачи 30.18
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
30.16 Пружина имеет в ненапряженном состоянии длину 20 см. Сила, необходимая для изменения ее длины на 1 см, равна 1,96 Н. С какой скоростью v вылетит из трубки шарик массы 30 г, если пружина была сжата до длины 10 см? Трубка расположена горизонтально.
|
30.17 Статический прогиб балки, загруженной посередине грузом Q, равен 2 мм. Найти наибольший прогиб балки, пренебрегая ее массой, в двух случаях: 1) когда груз Q положен на неизогнутую балку и опущен без начальной скорости; 2) когда груз Q падает на середину неизогнутой балки с высоты 10 см без начальной скорости. При решении задачи следует иметь в виду, что сила, действующая на груз со стороны балки, пропорциональна ее прогибу.
|
30.19 Груз M веса P, подвешенный в точке O на нерастяжимой нити длины l, начинает двигаться в вертикальной плоскости без начальной скорости из точки A; при отсутствии сопротивления груз M достигнет положения C, где его скорость обратится в нуль. Приняв потенциальную энергию, обусловленную силой тяжести груза M в точке B, равной нулю, построить графики изменений кинетической и потенциальной энергии, а также их суммы в зависимости от угла φ. Массой нити пренебречь.
|
30.20 Материальная точка массы m совершает гармонические колебания по прямой Ox под действием упругой восстанавливающей силы по следующему закону: x=a sin(kt+β). Пренебрегая сопротивлениями, построить графики изменения кинетической энергии T и потенциальной энергии V движущейся точки в зависимости от координаты x; в начале координат V=0.
|
|