Решение задач → Задачи по теоретической механике с решениями
Коническое зубчатое колесо, ось которого пересекается с геометрической осью плоской опорной шестерни в центре последней, обегает пять раз в минуту опорную шестерню. Определить угловую скорость ωr вращения колеса вокруг его оси и угловую скорость ω вращения вокруг мгновенной оси, если радиус опорной шестерни вдвое больше радиуса колеса: R=2r.
Для просмотра изображения в полном размере нажмите на него 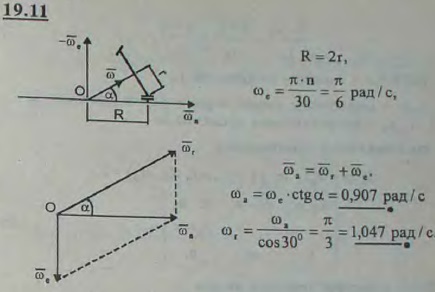 |
Решение задачи 19.11
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
19.9 Диск OA радиуса R=4√3 см, вращаясь вокруг неподвижной точки O, обкатывает неподвижный конус с углом при вершине, равным 60°. Найти угловую скорость вращения диска вокруг его оси симметрии, если ускорение wA точки A диска по модулю постоянно и равно 48 см/с2.
|
19.10 Тело движется вокруг неподвижной точки. В некоторый момент угловая скорость его изображается вектором, проекции которого на координатные оси равны √3, √5, √7. Найти в этот момент скорость v точки тела, определяемой координатами √12, √20, √28.
|
19.12 Угловая скорость тела ω=7 рад/с, мгновенная ось его составляет в данный момент с неподвижными координатными осями острые углы α, β и γ. Найти величину скорости v и проекции ее vx, vy, vz на координатные оси для точки тела, координаты которой, выраженные в метрах, в данный момент равны 0, 2, 0, а также расстояние d этой точки от мгновенной оси, если cos α=2/7, cos γ=6/7.
|
19.13 Найти уравнения мгновенной оси и величину угловой скорости ω тела, если известно, что проекции скорости точки M1(0;0;2) на координатные оси, связанные с телом, равны vx1=1 м/с, vy1=2 м/с, vz1=0, а направление скорости точки M2(0;1;2) определяется косинусами углов, образованных с осями координат:-2/3, +2/3,-1/3.
|
|