Решение задач → Задачи по теоретической механике с решениями
На рисунке изображен суммирующий механизм. В него входят стержни 1 и 2, движущиеся вдоль вертикальных направляющих. Эти стержни соединены с коромыслом AB цилиндрическими шарнирами, скользящими в пазах коромысла. Стержни движутся со скоростями v1 и v2. Показать, что скорость стержня 3, соединенного с центром O коромысла AB и скользящего в вертикальных направляющих, равна по модулю
v=bv1/(a+b) + av2/(a+b),
где a и b-размеры, указанные на рисунке. Найти также угловую скорость коромысла AB.
Для просмотра изображения в полном размере нажмите на него 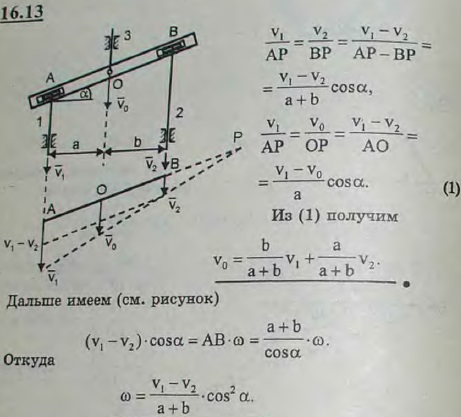 |
Решение задачи 16.13
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
16.11 Стержень AB длины 0,5 м движется в плоскости рисунка. Скорость vA (vA=2 м/с) образует угол 45° с осью x, совмещенной со стержнем. Скорость vB точки B образует угол 60° с осью x. Найти модуль скорости точки B и угловую скорость стержня.
|
16.12 Точильный станок приводится в движение педалью OA=24 см, которая колеблется около оси O по закону φ=(π/6)sin(πt/2) рад (угол φ отсчитывается от горизонтали). Точильный камень K вращается вокруг оси O1 с помощью стержня AB. Оси O и O1 перпендикулярны плоскости рисунка. Найти скорость точки D, лежащей на ободе точильного камня K радиуса R=2BO1, при t=0, если в этот момент OA и O1B расположены горизонтально.
|
16.14 Стержень OB вращается вокруг оси O с постоянной угловой скоростью ω=2 с-1 и приводит в движение стержень AD, точки A и C которого движутся по осям: A-по горизонтальной Ox, C-по вертикальной Oy. Определить скорость точки D стержня при φ=45° и найти уравнение траектории этой точки, если AB=OB=BC=CD=12 см.
|
16.15 В кривошипном механизме длина кривошипа OA=40 см, длина шатуна AB=2 м; кривошип вращается равномерно с угловой скоростью, равной 6π рад/с. Найти угловую скорость ω шатуна и скорость средней его точки M при четырех положениях кривошипа, для которых угол AOB соответственно равен 0, π/2, π, Зπ/2.
|
|
