Решение задач → Задачи по теоретической механике с решениями
Для переправы через реку устроена люлька L, которая посредством ролика C подвешена к стальному тросу AB, закрепленному в вершинах башен A и B. Для передвижения ролика C к левому берегу служит канат CAD, перекинутый через блок A и наматываемый на ворот D; такой же канат имеется для подтягивания люльки к правому берегу. Точки A и B находятся на одной горизонтали на расстоянии AB=100 м одна от другой; длина троса ACB равна 102 м; вес люльки 50 кН. Пренебрегая весом канатов и троса, а также трением ролика о трос, определить натяжение каната CAD и натяжение троса ACB в тот момент, когда длина ветви AC=20 м
Для просмотра изображения в полном размере нажмите на него 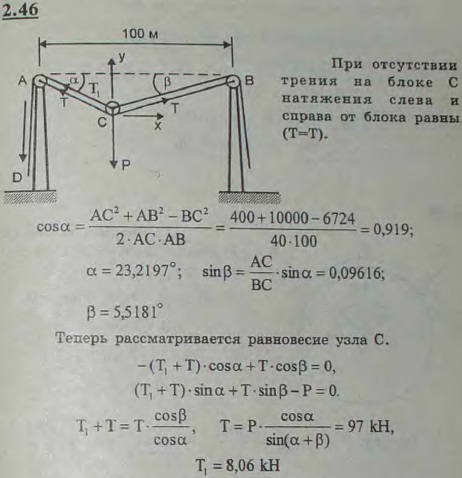 |
Решение задачи 2.46
(Мещерский И.В.)
| << Предыдущее
|
Следующее >>
|
|
2.44. Кран состоит из неподвижной башни AC и подвижной фермы BC, которая имеет шарнир C и удерживается тросом AB. Груз Q=40 кН висит на цепи, перекинутой через блок в точке B и идущей к вороту по прямой BC. Длина AC=BC. Определить, пренебрегая весом фермы и трением на блоке, натяжение T троса AB и силу P, сжимающую ферму по прямой BC, как функции угла ACB=φ
|
2.45. Блок C с грузом P=18 Н может скользить вдоль гибкого троса ACB, концы которого A и B прикреплены к стенам. Расстояние между стенами 4 м; длина троса 5 м. Определить натяжение троса при равновесии блока с грузом, пренебрегая весом троса и трением блока о трос. Натяжения частей троса AC и CB одинаковы; их величина может быть определена из подобия треугольника сил и равнобедренного треугольника, одна из боковых сторон которого есть прямая BCE, а основание лежит на вертикали BD
|
2.47. Оконная рама AB, изображенная на рисунке в разрезе, веса 100 Н, открывается, вращаясь вокруг горизонтальной оси A, при помощи шнура BCD, огибающего блоки C и D. Блок C, размерами которого пренебрегаем, и точка A лежат на одной вертикали; вес рамы приложен в ее середине; трением также пренебрегаем. Найти натяжение T шнура в зависимости от угла φ, образуемого рамой AB с горизонталью AH, предполагая AB=AC, а также наибольшее и наименьшее значения этого натяжения
|
2.48. На круглом гладком цилиндре с горизонтальной осью и радиуса OA=0,1 м лежат два шарика A и B; вес первого 1 Н, второго 2 Н. Шарики соединены нитью AB длины 0,2 м. Определить углы φ1 и φ2, составляемые радиусами OA и OB с вертикальной прямой OC в положении равновесия, и давления N1 и N2 шариков на цилиндр в точках A и B. Размерами шариков пренебречь
|
|