Решение задач → Задачи по геометрии с решениями
Четыре параллельные прямые пересекают параллельные плоскости в вершинах параллелограммов ABCD и A1B1C1D1 соответственно. Докажите, что параллелограммы ABCD и A1B1C1D1 совмещаются параллельным переносом.
Для просмотра изображения в полном размере нажмите на него 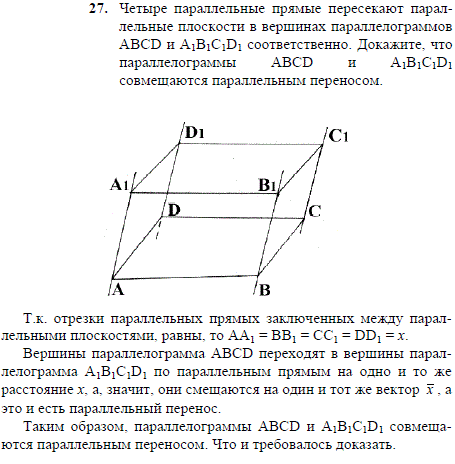 |
Решение задачи
(Погорелов А.В. 10 класс)
| << Предыдущее
|
Следующее >>
|
|
Существует ли параллельный перенос, при котором точка A переходит в точку B, а точка C-в точку D, если: 1) A(2;1;0), B(1;0;1), C(3;-2;1), D(2;-3;0); 2) A(-2;3;5), B(1;2;4), C(4;-3;6), D(7;-2;5); 3) A(0;1;2), B(-1;0;1), C(3;-2;2), D(2;-3;1) 4) A(1;1;0), B(0;0;0), C(-2;2;1), D(1;1;1)
|
Докажите, что при параллельном переносе параллелограмм переходит в равный ему параллелограмм.
|
Докажите, что преобразование гомотетии в пространстве является преобразованием подобия.
|
Три прямые, проходящие через точку S, пересекают данную плоскость в точках A, B, C, а параллельную ей плоскость в точках A1, B1, C1. Докажите, что треугольники ABC и A1B1C1 гомотетичны.
|
|