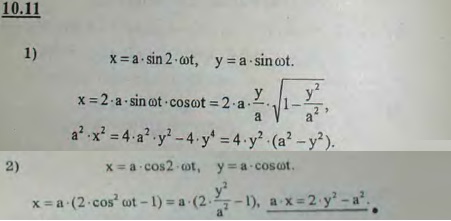Найти уравнение траектории движения точки, получающегося при сложении взаимно перпендикулярных колебаний разной частоты: 1) x=a sin 2ωt, y=a

Поиск задач

Найти задачу можно, введя ее условие. Если с первого раза не нашли решение на нужное готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия

Решение задач → Задачи по теоретической механике с решениями

Найти уравнение траектории движения точки, получающегося при сложении взаимно перпендикулярных колебаний разной частоты:
1) x=a sin 2ωt, y=a sin ωt;
2) x=a cos 2ωt, y=a cos ωt.

Для просмотра изображения в полном размере нажмите на него

Найти уравнение траектории движения точки, получающегося при сложении взаимно перпендикулярных колебаний разной частоты: 1) x=a sin 2ωt, y=a

Решение задачи 10.11
(Мещерский И.В.)

<< Предыдущее

Следующее >>

10.9 Груз, поднятый на упругом канате, колеблется согласно уравнению x=a sin(kt+Зπ/2), где a-в сантиметрах, k-в рад/с. Определить амплитуду и круговую частоту колебаний груза, если период колебаний равен 0,4 с и в начальный момент x0=-4 см. Построить также кривую расстояний.

10.10 Определить траекторию точки, совершающей одновременно два гармонических колебания равной частоты, но разных амплитуд и фаз, если колебания происходят по двум взаимно перпендикулярным осям: x=a sin(kt+α), y=b sin(kt+β).

10.12 Кривошип OA вращается с постоянной угловой скоростью ω=10 рад/с. Длина OA=AB=80 см. Найти уравнения движения и траекторию средней точки M шатуна, а также уравнение движения ползуна B, если в начальный момент ползун находился в крайнем правом положении; оси координат указаны на рисунке.

10.13 Определить уравнения движения и траекторию точки обода колеса радиуса R=1 м автомобиля, если автомобиль движется по прямолинейному пути с постоянной скоростью 20 м/с. Принять, что колесо катится без скольжения; за начало координат взять начальное положение точки на пути, принятом за ось Ox.

online-tusa.com | SHOP