Докажите, что преобразование симметрии относительно координатной плоскости xy задается формулами x'=x, y'=y, z'=-z.

Поиск задач

Найти задачу можно, введя ее условие. Если с первого раза не нашли решение на нужное готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия

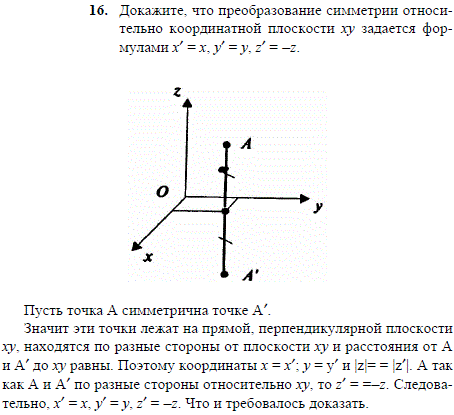
Решение задач → Задачи по геометрии с решениями

Для просмотра изображения в полном размере нажмите на него

Решение задачи
(Погорелов А.В. 10 класс)

<< Предыдущее

Следующее >>

Докажите, что середина отрезка с концами в точках A(a;c;-b) и B(-a;d;b) лежит на оси y

Докажите, что середина отрезка с концами в точках C(a;b;c) и D(p;q;-c) лежит в плоскости xy.

Даны точки (1;2;3), (0;-1;2), (1;0;-3). Найдите точки, симметричные данным относительно координатных плоскостей.

Даны точки (1;2;3), (0;-1;2), (1;0;-3). Найдите точки, симметричные им относительно начала координат.