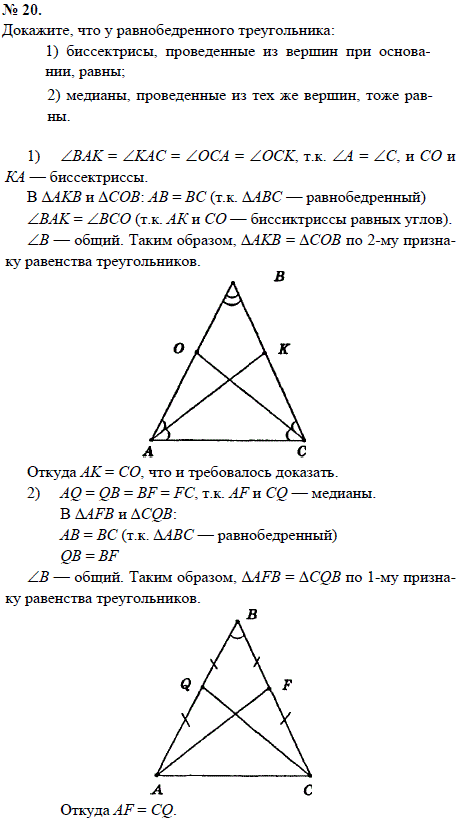
Докажите, что у равнобедренного треугольника: 1) биссектрисы, проведенные из вершин при основании, равны; 2) медианы, проведенные из тех же вершин

Поиск задач

Найти задачу можно, введя ее условие. Если с первого раза не нашли решение на нужное готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия

Решение задач → Задачи по геометрии с решениями

Докажите, что у равнобедренного треугольника:
1) биссектрисы, проведенные из вершин при основании, равны;
2) медианы, проведенные из тех же вершин, тоже равны

Для просмотра изображения в полном размере нажмите на него

Решение задачи
(Погорелов А.В. 7 класс)

<< Предыдущее

Следующее >>

На сторонах AC и BC треугольника ABC взяты точки С1 и С2. Докажите, что треугольник ABC равнобедренный, если треугольники ABC1 и ВАС2 равны

1) Докажите, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника. 2) Докажите, что середины сторон равностороннего треугольника являются также вершинами равностороннего треугольника

Докажите, что у равных треугольников АВС и А1В1С1: 1) медианы, проведенные из вершин А и А1, равны; 2) биссектрисы, проведенные из вершин А и А1, равны

Точки А, С, В, D лежат на одной прямой, причем отрезки АВ и CD имеют общую середину. Докажите, что если треугольник АВЕ равнобедренный с основанием АВ, то треугольник CDE тоже равнобедренный с основанием CD

online-tusa.com | SHOP